Trigyrate rhombicosidodecahedron
Appearance
| Trigyrate rhombicosidodecahedron | |
|---|---|
 | |
| Type | Johnson J74 – J75 – J76 |
| Faces | 2+2x3+2x6 triangles 4x3+3x6 squares 4x3 pentagons |
| Edges | 120 |
| Vertices | 60 |
| Vertex configuration | 5x6(3.42.5) 4x3+3x6(3.4.5.4) |
| Symmetry group | C3v |
| Dual polyhedron | - |
| Properties | convex, canonical |
| Net | |
 | |

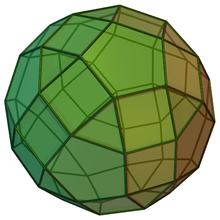
In geometry, the trigyrate rhombicosidodecahedron is one of the Johnson solids (J75). It contains 20 triangles, 30 squares and 12 pentagons. It is also a canonical polyhedron.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
It can be constructed as a rhombicosidodecahedron with three pentagonal cupolae rotated through 36 degrees. Related Johnson solids are:
- The gyrate rhombicosidodecahedron (J72) where one cupola is rotated;
- The parabigyrate rhombicosidodecahedron (J73) where two opposing cupolae are rotated;
- And the metabigyrate rhombicosidodecahedron (J74) where two non-opposing cupolae are rotated.
References
[edit]- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
External links
[edit]
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
