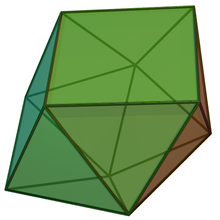
Sphenocorona
| Sphenocorona | |
|---|---|
 | |
| Type | Johnson J85 – J86 – J87 |
| Faces | 12 triangles 2 squares |
| Edges | 22 |
| Vertices | 10 |
| Vertex configuration | 4(33.4) 2(32.42) 2x2(35) |
| Symmetry group | C2v |
| Dual polyhedron | - |
| Properties | convex, elementary |
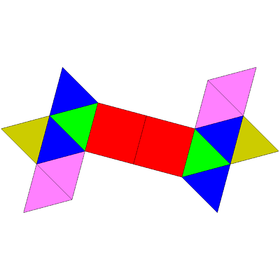
| Net | |
 | |

In geometry, the sphenocorona is a Johnson solid with 12 equilateral triangles and 2 squares as its faces.
Properties
[edit]The sphenocorona was named by Johnson (1966) in which he used the prefix spheno- referring to a wedge-like complex formed by two adjacent lunes—a square with equilateral triangles attached on its opposite sides. The suffix -corona refers to a crownlike complex of 8 equilateral triangles.[1] By joining both complexes together, the resulting polyhedron has 12 equilateral triangles and 2 squares, making 14 faces.[2] A convex polyhedron in which all faces are regular polygons is called a Johnson solid. The sphenocorona is among them, enumerated as the 86th Johnson solid .[3] It is an elementary polyhedron, meaning it cannot be separated by a plane into two small regular-faced polyhedra.[4]
The surface area of a sphenocorona with edge length can be calculated as:[2] and its volume as:[2]
Cartesian coordinates
[edit]Let be the smallest positive root of the quartic polynomial . Then, Cartesian coordinates of a sphenocorona with edge length 2 are given by the union of the orbits of the points under the action of the group generated by reflections about the xz-plane and the yz-plane.[5]
Variations
[edit]The sphenocorona is also the vertex figure of the isogonal n-gonal double antiprismoid where n is an odd number greater than one, including the grand antiprism with pairs of trapezoid rather than square faces.
See also
[edit]References
[edit]- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, S2CID 122006114, Zbl 0132.14603
- ^ a b c Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245
- ^ Francis, Darryl (2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177
- ^ Cromwell, P. R. (1997), Polyhedra, Cambridge University Press, p. 86–87, 89, ISBN 978-0-521-66405-9
- ^ Timofeenko, A. V. (2009), "The non-Platonic and non-Archimedean noncomposite polyhedra", Journal of Mathematical Science, 162 (5): 718, doi:10.1007/s10958-009-9655-0, S2CID 120114341
External links
[edit]- Weisstein, Eric W., "Sphenocorona" ("Johnson solid") at MathWorld.