Jump to content

Penrose stairs

From Wikipedia, the free encyclopedia
Penrose stairs

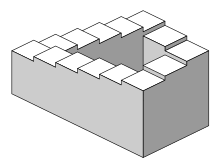
The Penrose stairs or Penrose steps, also dubbed the impossible staircase, is an impossible object created by Oscar Reutersvärd in 1937[1][2][3][4] and later independently discovered and made popular by Lionel Penrose and his son Roger Penrose.[5] A variation on the Penrose triangle, it is a two-dimensional depiction of a staircase in which the stairs make four 90-degree turns as they ascend or descend yet form a continuous loop, so that a person could climb them forever and never get any higher. This is clearly impossible in three-dimensional Euclidean geometry but possible in some non-Euclidean geometry like in nil geometry.[6]

The "continuous staircase" was first presented in an article that the Penroses wrote in 1959, based on the so-called "triangle of Penrose" published by Roger Penrose in the British Journal of Psychology in 1958.[5] M.C. Escher then discovered the Penrose stairs in the following year and made his now famous lithograph Klimmen en dalen (Ascending and Descending) in March 1960. Penrose and Escher were informed of each other's work that same year.[7] Escher developed the theme further in his print Waterval (Waterfall), which appeared in 1961.

In their original article the Penroses noted that "each part of the structure is acceptable as representing a flight of steps but the connections are such that the picture, as a whole, is inconsistent: the steps continually descend in a clockwise direction."[8]

History of discovery

[edit]

The Penroses

[edit]
Ascending and Descending by M. C. Escher

Escher, in the 1950s, had not yet drawn any impossible stairs and was not aware of their existence. Roger Penrose had been introduced to Escher's work at the International Congress of Mathematicians in Amsterdam in 1954. He was "absolutely spellbound" by Escher's work, and on his journey back to England he decided to produce something "impossible" on his own. After experimenting with various designs of bars overlying each other he finally arrived at the impossible triangle. Roger showed his drawings to his father, who immediately produced several variants, including the impossible flight of stairs. They wanted to publish their findings but did not know in what field the subject belonged. Because Lionel Penrose knew the editor of the British Journal of Psychology and convinced him to publish their short manuscript, the finding was finally presented as a psychological subject. After the publication in 1958 the Penroses sent a copy of the article to Escher as a token of their esteem.[9]

While the Penroses credited Escher in their article, Escher noted in a letter to his son in January 1960 that he was:

working on the design of a new picture, which featured a flight of stairs which only ever ascended or descended, depending on how you saw it. [The stairs] form a closed, circular construction, rather like a snake biting its own tail. And yet they can be drawn in correct perspective: each step higher (or lower) than the previous one. [...] I discovered the principle in an article which was sent to me, and in which I myself was named as the maker of various 'impossible objects'. But I was not familiar with the continuous steps of which the author had included a clear, if perfunctory, sketch, although I was employing some of his other examples.[10]

Escher was captivated by the endless stairs and subsequently wrote a letter to the Penroses in April 1960:

A few months ago, a friend of mine sent me a photocopy of your article... Your figures 3 and 4, the 'continuous flight of steps', were entirely new to me, and I was so taken by the idea that they recently inspired me to produce a new picture, which I would like to send to you as a token of my esteem. Should you have published other articles on impossible objects or related topics, or should you know of any such articles, I would be most grateful if you could send me further details.[10]

At an conference in Rome in 1985, Roger Penrose said that he had been greatly inspired by Escher's work when he and his father discovered both the Penrose tribar structure (that is, the Penrose triangle) and the continuous steps.

Oscar Reutersvärd

[edit]

The staircase design had been discovered previously by the Swedish artist Oscar Reutersvärd, but neither Penrose nor Escher was aware of his designs.[4] Inspired by a radio programme on Mozart's method of composition—described as "creative automatism"; that is, each creative idea written down inspired a new idea—Reutersvärd started to draw a series of impossible objects on a journey from Stockholm to Paris in 1950 in the same "unconscious, automatic" way. He did not realize that his figure was a continuous flight of stairs while drawing, but the process enabled him to trace his increasingly complex designs step by step. When M.C. Escher's Ascending and Descending was sent to Reutersvärd in 1961, he was impressed but didn't like the irregularities of the stairs (2 × 15 + 2 × 9). Throughout the 1960s, Reutersvärd sent several letters to Escher to express his admiration for his work, but the Dutch artist failed to respond.[11] Roger Penrose only discovered Reutersvärd's work in 1984.[9]

Escherian Stairwell

[edit]

The Escherian Stairwell is a viral video based on the Penrose stairs illusion. The video, filmed at Rochester Institute of Technology by Michael Lacanilao, was edited to create a seemingly cyclic stairwell such that if someone walks in either direction, they will end up where they started.[12] The video claims that the stairwell, whose name evokes M.C. Escher's impossible objects, was built in the 1960s by the fictitious architect Rafael Nelson Aboganda. The video was revealed to be an Internet hoax, as individuals have travelled to Rochester Institute of Technology to view the staircase.[13]

[edit]
  • The Penrose stairs appeared twice in the movie Inception. This paradoxical illusion can only be realized in the dream worlds of the film. In the film, the hero descends the stairs fleeing from a guard. In the real world, the hero should always be in front of the villain throughout this chase. However, in the case of the Penrose stairs the hero descends another flight of stairs to catch up to the antagonist and catch him unaware.[14]
  • The cover of the 2011 album Angles by American rock band The Strokes depicts a complex set of Penrose stairs.
  • In their 2015 single called "Greek Tragedy," English rock band The Wombats mentions the Penrose steps.[15]

See also

[edit]
Wikimedia Commons has media related to Penrose figures.

Notes

[edit]
  1. ^ Penrose Stairs. Benedikt Taschen. 1992. ISBN 9783822896372. Archived from the original on 23 November 2022. Retrieved 9 October 2020.
  2. ^ Torre, Matteo. "Impossible Pictures: When Art Helps Math Education" (PDF). Impossible Pictures: When Art Helps Math Education. Archived (PDF) from the original on 20 March 2020. Retrieved 9 October 2020.
  3. ^ "Endless staircase". Impossible World. Archived from the original on 6 July 2020. Retrieved 9 October 2020.
  4. ^ a b IllusionWorks 1997
  5. ^ a b Penrose & Penrose 1958, pp. 31–33
  6. ^ YouTube, ZenoTheRogue, Ascending and Descending in Nil, archived from the original on 2022-07-09, retrieved 2022-07-09
  7. ^ Hallyn 2000, p. 172
  8. ^ Ernst 1992, p. 72
  9. ^ a b Ernst 1992, pp. 71–72
  10. ^ a b Ernst 1992, pp. 75, 78
  11. ^ Ernst 1992, pp. 70–71
  12. ^ Schwartz, Heidi (17 May 2013). "The Escherian Stairwell (Penrose Steps) | How It Works". Facility Executive - Creating Intelligent Buildings. Archived from the original on 18 April 2019. Retrieved 18 April 2019.
  13. ^ Mikkelson, David (6 May 2013). "FACT CHECK: Escherian Stairwell". Snopes.com. Archived from the original on 20 May 2022. Retrieved 18 April 2019.
    Melikdjanian, Alan (2018), "Escherian Stairwell Deconstruction", Captain Disillusion, archived from the original on 2023-05-05, retrieved 2023-05-05 – via YouTube
  14. ^ Harshbarger, Eric (2010-08-19). "The Never-Ending Stories: Inception's Penrose Staircase". Wired. ISSN 1059-1028. Archived from the original on 2015-10-22. Retrieved 2020-06-05.
  15. ^ "Greek Tragedy". Genius. Retrieved 25 October 2023.

References

[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Penrose_stairs&oldid=1261172926"